Вычислить высоту стола кошка черепаха

Какой высоты стол? Задачка для китайских учеников начальной школы всполошила Интернет

В сентябре 2018 года в Твиттер-аккаунте China_Focus была опубликована одна любопытная математическая задачка, предназначенная для детей. Она стала проблемой для учеников начальных классов китайской средней школы. Однако такое задание вполне может поставить в тупик любого взрослого. В сети Интернет мгновенно появились различные варианты решения задачки. Давайте попробуем решить ее вместе.

Исходные данные

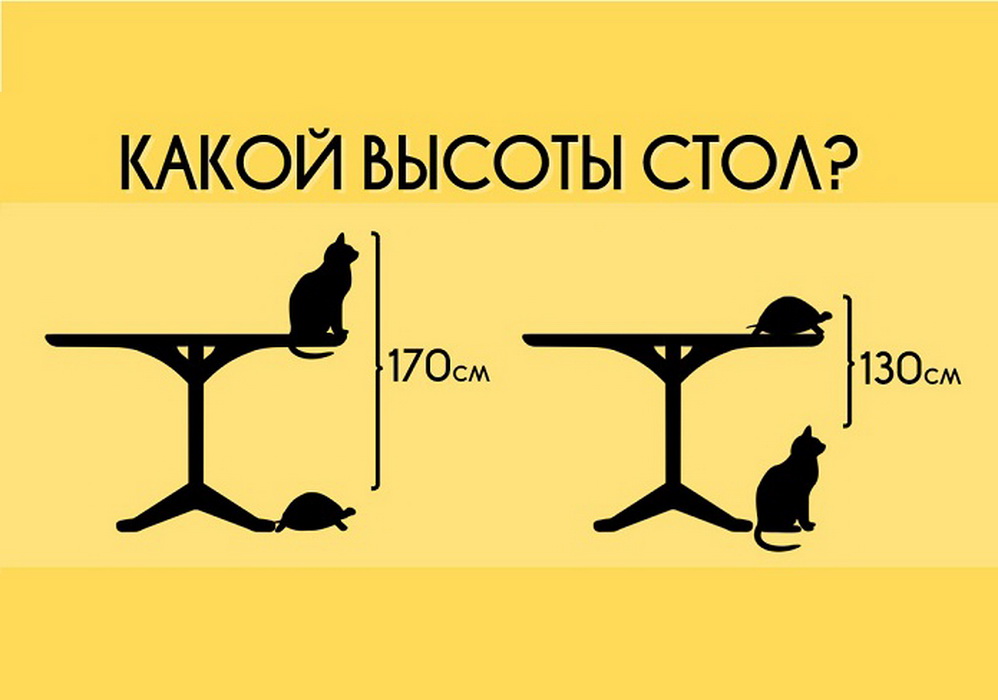
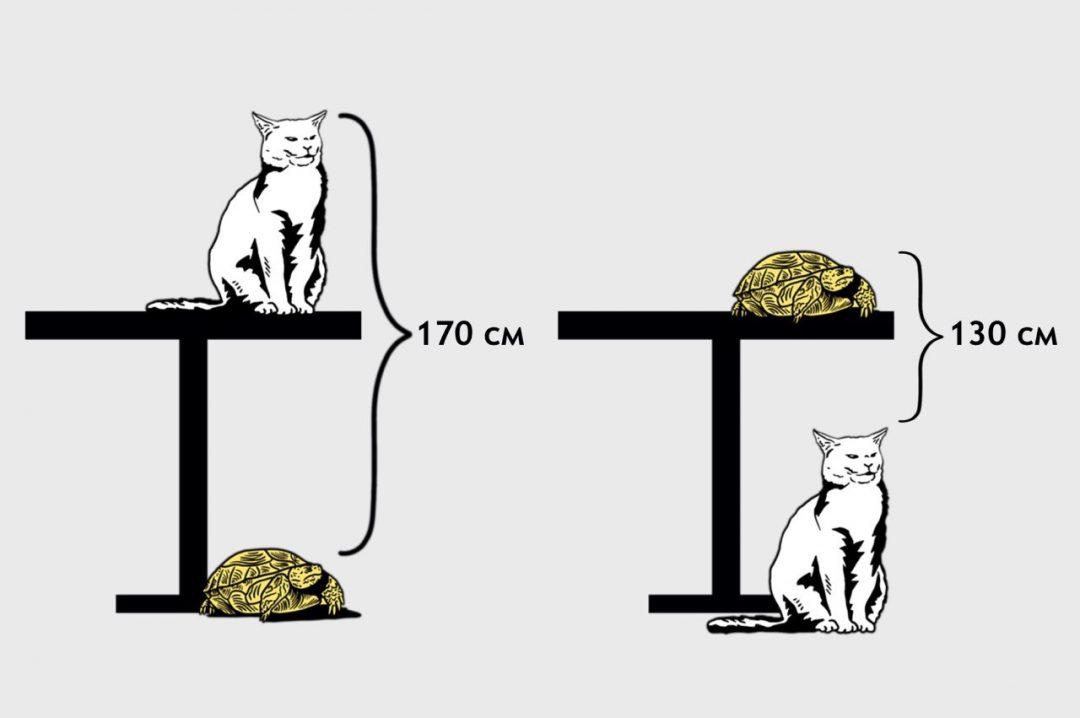
В первоначальном варианте в Твиттере на рисунках изображены два кота, на одном из которых один кот стоит под столом, а второй лежит на столе. На втором рисунке коты меняют свои положения: тот, который лежал, встает, а тот, который стоял, ложится.

Изменим немного условие задачи. Итак, перед нами два рисунка, на которых отмечено расстояние между двумя животными: черепахой и котом. На первом рисунке черепаха сидит под столом, а кот – на столе. На втором рисунке животные меняются местами: кот спускается под стол, а черепаха, наоборот, взбирается на него.

Первый способ решения задачи

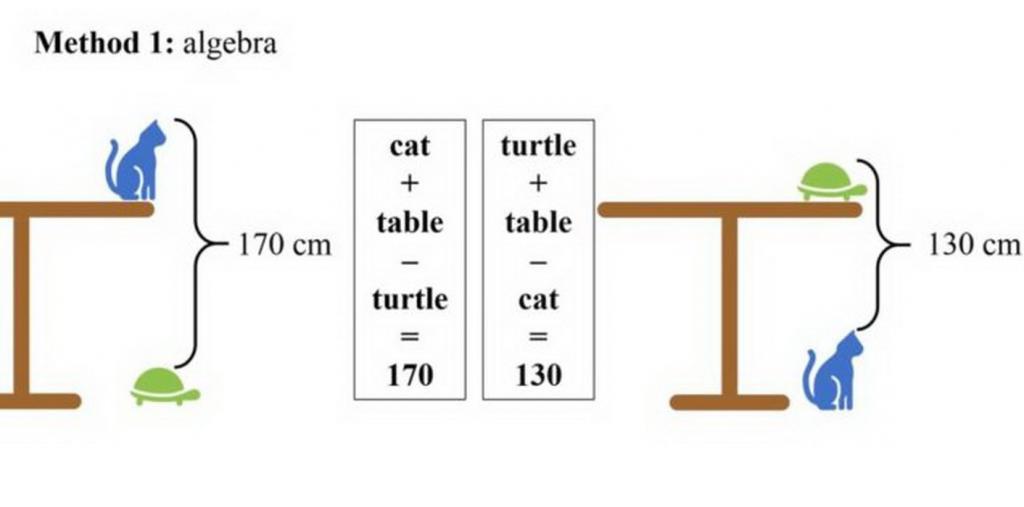
Для решения этой задачи нам на помощь придет алгебра. В соответствии с исходными данными составим два уравнения – по одному для каждого рисунка.

Для начала введем некоторые обозначения:

На рисунке слева к высоте стола прибавляется высота кота и отнимается высота черепахи:

К + С – Ч = 170 см.

На рисунке справа к высоте стола прибавляется высота черепахи и отнимается высота кота:

Ч + С – К = 130 см.

Складываем уравнения друг с другом:

К + С – Ч + Ч + С – К = 170 + 130 (см).

Ответ: высота стола составляет 150 см.

Второй метод решения задачи

Тяжело сказать, насколько хорошо китайские студенты знают алгебру, поэтому попробуем другой вариант решения задачи.

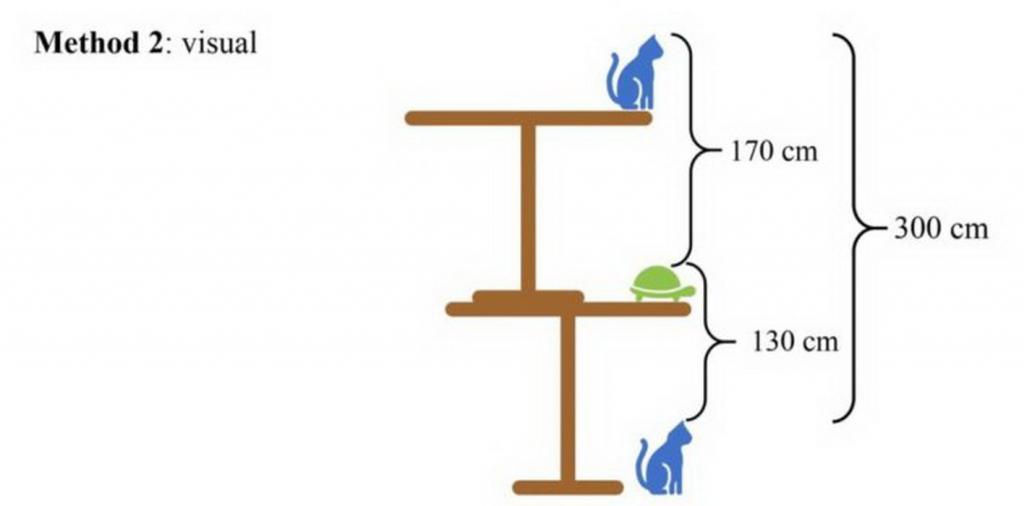
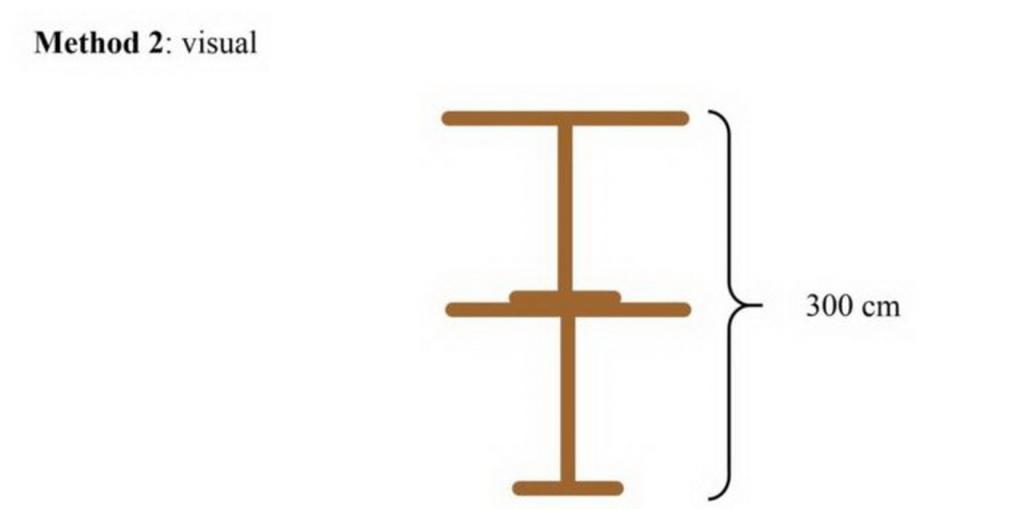
Данный метод предполагает схематическое решение. Один рисунок накладывается сверху на второй таким способом, чтобы два расстояния можно было сложить между собой.

В результате получается, что расстояние от головы кота на нижней части получившегося рисунка до головы кота, расположенного в верхней части этого рисунка, составляет 300 см. Такое же расстояние будет и от лап первого кота до лап второго, поскольку высота кота является величиной постоянной. Поэтому, можно нарисовать третью схему, на которой вообще не будет животных. В соответствии с ней высота двух столов составляет 300 см. Отсюда легко установить, что один стол имеет высоту 150 см.

Если вы правильно поняли ход решения задачи, теперь на подобные задания у вас будет уходить всего несколько секунд. В исходном варианте были предложены расстояния 110 и 150 см соответственно. Отсюда без проблем можно определить, что высота «китайского» стола составляет 130 см.

Источник

Какой высоты стол?

Китайская задача про стол, кота, черепаху и взрыв мозга.

Вот задачка, от которой перегревается процессор у многих взрослых. Хотя всю задачу можно описать одной картинкой:

Какой высоты стол?

Может показаться, что эта задача не имеет решения: мы не знаем ничего о размерах кота и черепахи, только разницу в высоте. Но так ли это на самом деле?

Обозначим высоту стола за С, черепахи — Ч, а кота — К. Теперь запишем то, что на картинках, в виде математических формул.

На первой картинке кот сидит на столе (К + С), и нам нужно отнять от этого высоту черепахи (Ч), чтобы получить 170 сантиметров:

На второй — черепаха сидит на столе (Ч + С), и нам нужно отнять высоту кота (К), чтобы получилось 130 сантиметров:

Теперь у нас есть два уравнения и три неизвестных. Любой математик скажет, что такая система не имеет решения, и будет прав. Но нам не нужны все три неизвестных, чтобы решить задачу, нам достаточно найти высоту стола! Воспользуемся этим и вынесем С в каждом уравнении:

Сложим оба уравнения:

2С = 170 + 130 + К – К + Ч – Ч

Смотрите, у нас сокращаются К и Ч, потому что мы их одновременно складываем и вычитаем. Получаем такое:

2С = 170 + 130 = 300

Вот и ответ! Высота стола — 150 сантиметров.

Усложняем

Теперь, когда вы знаете решение, попробуйте найти высоту кота и черепахи.

Эта задача решается не так просто, как кажется.

Эта задача поставит в тупик половину интернета, но не вас.

Заходят как-то в бар два интроверта.

На этот раз у него 49 проводов, но он справится.

Раскрась кубик правильно.

Чтобы победить, не нужно уворачиваться от врагов в слоу-мо. Иногда нужно просто знать теорию вероятностей.

Это сложно, но можно

Как одним вопросом получить ОЧЕНЬ МНОГО информации.

Когда вы решили все логические задачи на собеседовании, вам предложат последнюю — самую важную.

Задачка на геометрию.

Непростая задачка против звериного оскала капитализма.

Сложная задача с несложной математикой

Программистская задача с математическим уклоном.

Источник

Задачка про кота, стол и черепаху взорвет вам мозг. Но решение простое

Условие задачи

В начальной школе Китая школьникам предлагают решить такую задачку: высота от панциря стоящей на полу черепахи до макушки кота, сидящего на столе, составляет 170 см. А высота от черепахи на столе до головы кота, сидящего на полу, равна 130 см.

Вопрос: какой высоты стол?

Внимание! Под картинкой ниже будет решение.

Есть два способа решения

Первый способ

Первую картинку можно перевести в равенство: кот + стол – черепаха = 170. Вторую – в равенство: черепаха + стол – кот = 130. Вместе эти равенства составят систему уравнений, в которых кота и черепаху можно сократить, а столы сложить и получить уравнение 2стола = 300, из которого станет ясно, что высота одного стола равна 150 см:

Второй способ

Второй способ решения — визуальный.

Представьте, как эти две картинки накладываются одна на другую по «линии черепах». Получится, что расстояние от макушки кота, сидящего на полу, до макушки кота, сидящего на столе, равно 300 см.

Если удалить животных с картинки и опустить мерку до уровня первого пола, получится, что 300 см – это высота двух столов. В итоге, останется только разделить это число на два и найти высоту одного стола – 150 см.

Источник

Задача о столе, коте, черепахе, бутылке и стакане . Как решить?

Дано: расстояние от головы черепахи, сидящей столом, до головы кота на столе равна 170 см , расстояние от головы кота, сидящего под столом, до головы черепахи на столе — 130 см . Предлагается вычислить высоту стола.

Какие есть способы решения?

Решение. Пусть высота стола, кота и черепахи равны С , К и Ч, соответственно. Исходя из рисунка можно заключить :

С+К-Ч = 170 и С +Ч-К = 130. Если сложить оба уравнения, то С +К-Ч+С+Ч-К = 2С = 170+130 = 300, то есть С = 300/2 = 150.

Чтобы вычислить высоту стола нужно или исключить из расчета черепаху с ее ростом, оставив кота вместе со столом или отсоединить от стола кота, оставив черепаху со столом, потом оба результата сложить и поделить пополам.

В сети предлагается как минимум два решения.

«Складываем» кота, стол и вычитаем черепаху. Выходит 170 см .

Точно так же: черепаха + сто л- кот= 130 см .

Далее — вычеркиваем животных, остается 2 стола=300, следовательно, один — 150 см .

Второй способ — визуальный.

Накладываем параметры, совмещаем, остается 300/2=150.

Кот + Сто л- Черепаха = 170 см

Черепаха +Стол — кот = 130 см

Задачку можно решить просто без вычислений.

Сделаем сложение двух равенств:

Кот + Стол- Черепаха + Черепаха + Стол — Кот = 170 + 130

Итого: 2 Стола = 300 см

С первой картинки: к высоте кота прибавить высоту стола отнять высоту черепахи равно 170 сантиметров .

Во втором случае: высоту стола прибавить высоту черепахи минус высоту кота равно 130 сантиметров .

И получим систему уравнений с тремя неизвестными. Берем для обозначения первую букву слова, а не х с у.

Выражаем стол и в первом уравнении, и во втором.

Поскольку стол один и тот же, приравниваем эти два уравнения. Так остаются два неизвестных.

Определяем высоту кота

это высота черепахи плюс 20 сантиметров

И подставляем это в первое уравнение, поменяв кота на черепаху. Таким образом, можно сократить все до одного неизвестного. Можно это проделать и со вторых уравнением, разницы нет.

Отнимаем от черепахи другую черепаху и она исчезает.

Теперь остается один стол, размер которого и нужно узнать. При этом мы не знаем размеры черепахи и кота, но по условию от нас этого и не требуют.

Уж и не знаю, что так весь интернет взволновался по поводу задачи для учеников младших классов школ Китая, ничего там головоломного, в общем-то и нет.

Обозначаем высоту кота буквой К , высоту стола буквой С, а высоту черепахи — буквой Ч.

По двум картинкам составляем два уравнения.

Слева у нас будет К +С-Ч=170.

Сложим два эти уравнения:

сокращаем и получаем:

150 сантиметров получилось. Однако, необычный стол какой-то, очень высокий.

(В Китае ученики за партами стоят стоя)

170 см.+ 130 см .=300 см./2=150 см. Высота стола=150 см.

h стола — h черепахи + h кота = 170 см

h стола — h кота + h черепахи = 130 см

При сложении двух уравнений черепахи и коты, имеющие противоположные знаки сокращаются, а столы складываются

2h стола = 300 см

h стола = 150 см

Вот и всё решение.

Отсюда , вычтем одно равенство из другого ,получим: кот-черепаха=40+черепаха-кот.

Отсюда:2(кот-черепаха)=40 или: кот-черепаха=20.Находим высоту стола 170+черепаха-кот=170 -20=150.Что касается роста кота с черепахой то они могут быть разны е- черепаха от 0 до бесконечности( с точки зрения математики),кот от 20 см .также.

Задача непростая для младших школьников. Её можно решить 2мя способами. Один способ — это метод уравнений. Он не подойдет для младшеклассников , а второй — логический. А подробное решение, в том числе способ, которым могут решить дети, здесь .

2 расстояния стола равно 300 см (170 + 130). Отсюда одно расстояние стола — 150 см

Задача действительно на сообразительность, и действительно для младших классов, где не проходили понятия переменных x и y , тем более решений линейных уравнений с двумя неизвестными.

Всё выглядит гораздо проще, если посмотреть на рисунок. Имеем 2С=300 (см), или С( высота стола)=150 (см).

рост черепахи Ч=10 см, а кошки К =30см. Стол=150см; Решение: (130+К)-150=Ч; (170+Ч)-150 =К ; -10+К=Ч; 20+Ч=К; -10+20+Ч=Ч; Ч=10см; Тогда К=30см.

а как вы узнали, что черепаха 10? Все же, наверное, рост черепахи любой, а кошка на 20 см выше? : ) — 8

PS автор ошибся: Ч и Ч – сокращаются – уравнение не имеет решение. Задачу можно эту решить с двумя переменными, как и по одному рисунку с тремя переменными численным методом, где целевая функция ЦФ -> min с помощью организации циклов. Главное здесь правильно задать область ограничений и выхода из циклов при достижении минимума ЦФ.

Ограничение определяется довольно с помощью умозаключений (при условии, что высоту стола мы нашли):

Кот ограничения 20 кот 0

Определить размеры кота и черепахи, если известно, что высота стола 150

1) (К = 10) Высота черепахи Т = 150+10 -170 = -10 (высота черепахи не может быть отрицательно)

2) (К=20) Высота черепахи Т = 150+20-170 = 0 (высота черепахи тоже не может равняться 0)

3) (К=30) Высота черепахи Т = 150+30-170 = 10 (Проверка по правой картинке К = 150 +10 -130 = 30 — правильно)

4) (К=40) Высота черепахи Т = 150+40-170 = 20 (Проверка по правой картинке К = 150 +20 -130 = 40 — правильно)

5) (К=50) Высота черепахи Т = 150+50-170 =30 (Проверка по правой картинке К = 150 +30 -130 = 50 — правильно)

6) (К=60) Высота черепахи Т = 150+60-170 =40 (Проверка по правой картинке К = 150 +40 -130 = 60 — правильно)-

7) ( K =70) Высота черепахи Т = 150+70-170 =50 (Проверка по правой картинке К = 150 +50 -130 = 70 — правильно)

8) ( K =80 Высота черепахи Т = 150+80-170=60 (Проверка по правой картинке К = 150 +60 -130 = 80 — правильно)

9) ( K =90) Высота черепахи Т = 150+90-170=70 (Проверка по правой картинке К = 150 +70 -130 = 90 — правильно)

10) ( K =100) Высота черепахи Т = 150 +100 -170=80 (проверка по правой картинке К = 150 +80 -130 = 100 — правильно)

11) ( K =110) Высота черепахи Т = 150 +110 -170=90 (проверка по правой картинке К = 150 +90 -130 = 110 — правильно)

12) (К=120) Высота черепахи Т = 150 +120 -170=100 (проверка по правой картинке К = 150 +100 -130 = 120 — правильно)

13) ((К=130) Высота черепахи Т = 150 +130 -170=110 (проверка по правой картинке К = 150 +110 -130 = 130 — правильно)

14) (К=140) Высота черепахи Т = 150 +140 -170=120 (проверка по правой картинке К = 150 +120 -130 = 140 — правильно)

15) (К=150) Высота черепахи Т = 150 +150 -170=130 (проверка по правой картинке К = 150 +130 -130 = 150 — правильно)

20 10 и по ним решаем:

Пример 1. Решаем в системе Векторе: (ограничения максимальные) Получили: высота кота — К=75; высота черепахи — 55.

Проверка: по левой картинке: (К = 75) 150+75 – 170 = 55 (высота черепахи) Проверка К = 150 +55 -130 = 75 (высота кота) – правильно.

Пример 2 (ограничения максимальные) Расчет u =0.15 v = 0.15. Получили высота кота К = 70, черепахи T = 50 Проверка: (К = 70) 150+70 – 170 =50 (высота черепахи) Проверка К = 150 +50 -130 = 70 правильно

Поиск минимума ЦФ с изображением этого процесса

. Дан один рисунок. Определить высоту стола, высоту кота и высоту черепахи.

Неизвестны три переменных: высота кота – х , высота стола – y , высота черепахи – z .

.

График ЦФ и результаты расчета высоты кота, стола и черепахи – по данным первого рисунка.

При распитии стоя, высота стола вполне может быть 150 см, однако возьмем вариант, кода посетитель сидит.

Чему равна высота стола, стакана и бутылки,
в писательском кафе Рифей во Владивостоке?

Бутылку и стакан специально принесли для эксперимента. Бутылка, похоже, больше стандартной . Определить так ли это? Насколько больше?

Идею с бутылкой и стаканом « слямзили » с форума, на котором один из посетителей спрашивает: О чень интересно посмотреть на более развернутое решение примера. Наш ответ – как раз смотри выше с помощью задания целевой функции (ЦФ) (достаточно одной картинки) и трех циклов: перебрать, сравнить и выбрать.

В МК для кота и черепахи, изменяем область ограничений в ЦФ 170 на 120 и получаем:

Резюме: результаты получились не точно, но приемлемо. Например, округляем высоту стола до 100, далее по высоте стакана вычисляем высоту бутылки. Есть много вариантов улучшить результаты численного расчета. Главное надо понимать, как это делается, подкрепляя визуализацией входных параметров: область ограничения, диапазон изменения параметров U и V , построением ЦФ, с определением в какой момент она будет минимальной.

Высота стола и стакана известны Высота бутылки = 120+стакан-стол = 120+10-100=30.

В МК, чтобы исключить минусовый вариант, целевую функцию ( Hcf ) возводят в квадрат, вычисляя из нее корень квадратный.

Фрагмент макропрограммы с тремя неизвестными:

Smin =10000 ‘ заведомо большое число

For t =0.6 To 1.01 Step 1/21

Set p15 = PointOtr ( p1, p5, t)

Set p37 = PointOtr ( p3, p7, t)

Set p26 = PointOtr ( p2, p6, t)

Set p48 = PointOtr ( p4, p8, t)

For v=0.4 To 1.01 Step 1/21

Set p1537 = PointOtr ( p15, p37, v)

Set p2648 = PointOtr ( p26, p48, v)

For u=0.4 To 1.01 Step 1/21

Hcf = Sqr ( (Pt.x+Pt.y-Pt.z-120)*(Pt.x+Pt.y-Pt.z-120)) ‘ стремиться к нулю

if ( Hcf smin ) Then

Ngpoint.ss p( Pt.x,Pt.y,Pt.z-dlina /2)

otrezok.ss pt,p ( Pt.x,Pt.y,Pt.z-dlina /2)

So= DlinaOtr ( pt ,p ( Pt.x,Pt.y,Pt.z-dlina ))

VBSmsg » Бутылка : x = » & xmin & » Стол : y = » & ymin & » Стакан : z = » & zmin

Упражнение 1. Через поверхность вращения задать стакан с 14 гранями, Остальные параметры высоту, радиусы оснований взять произвольно

Пример 1. Бутылка треугольной формы через поверхность вращение, Образующая задается линией Безье (МК 4.12) или через команду Лини и- > Безье

Слева бутыль на комплексном чертеже, справа трехгранная каркас бутыли в аксонометрии

Упражнение 2 .Построить квадратную бутылку, высота которой h = 120+10 -100 = 30 (берем 3 см)

Источник